5. Sınıf Matematik Ders Kitabı Sayfa 51-52-53. Cevapları MEB Yayınları

5. Sınıf Matematik Ders Kitabı Sayfa 51-52-53. Cevapları MEB Yayınları bölümünde, ders kitabı sayfa 51-52-53 konularına ait cevapları bulabilirsiniz. “Üç Doğrunun Paralelliği Cevapları” ve “Üç Doğrunun Bir Noktada Kesişimi Cevapları” Sayfalarını hazırladık. Öğrenmenizi pekiştirmek ve anlamanızı kolaylaştırmak için 5. Sınıf Matematik Ders Kitabı Sayfa 51-52-53. Cevapları soruları dikkatlice inceleyin. Başarınızı arttırın.

Üç Doğrunun Paralelliği Cevapları

1.Ünite Geometrik Şekiller: 5. Sınıf Matematik Ders Kitabı Sayfa 51-52-53. Cevapları MEB Yayınları

5. Sınıf Matematik Ders Kitabı Sayfa 51 Cevapları MEB Yayınları

b) Bu iki durumu inceleyerek aşağıdaki tabloyu doldurunuz.
Cevap:

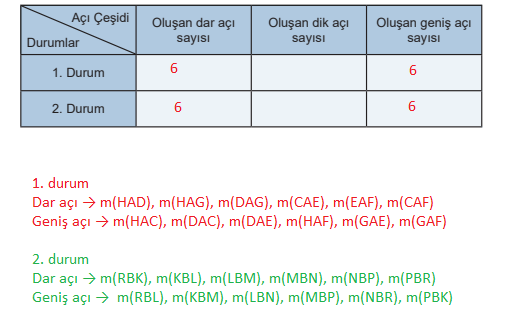
c) Bu iki durumda oluşan açı çeşitlerinin sayısına göre ulaştığınız çıkarımları ayrı ayrı yazınız.
Cevap: Açı çeşitleri birbirlerine eşittir.

Üç Doğrunun Paralelliği

a) Uçakların arkalarında bıraktığı egzoz izini doğru olarak düşününüz ve bu izlerin birbirlerine göre durumlarını yorumlayınız.
Cevap:Oluşan izler birbirlerine paraleldir.

b) Uçakların egzoz izleri üzerine doğrular çizip isimlendiriniz. Bu doğruların birbirlerine göre durumlarını sembolle ifade ediniz
Cevap:

Üç Doğrunun Bir Noktada Kesişimi Cevapları

5. Sınıf Matematik Ders Kitabı Sayfa 52 Cevapları MEB Yayınları

Yanda üç ana yolun buluştuğu kavşak görseli verilmiştir. Bu yolların üzerine birer doğru modeli çizilmiştir. Sizce kavşak neyi temsil eder? Yorumlayınız
Cevap:Kavşak yolların kesiştiği noktayı oluşturmaktadır.

Örnek 4

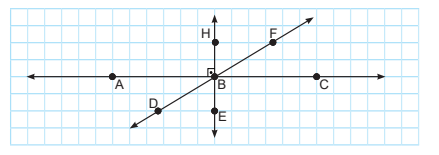
Asaf, defterine B noktasında kesişen AC, DF ve EH doğrularını yukarıdaki gibi çizmiştir. m(FBC) = 32°  olduğuna göre aşağıdaki soruları cevaplandırınız.

m(HBA) ve m(EBC) açıları eşittir.
90 + 90 = 180°

m(FBC) ve m(ABD) açıları eşittir.
32 + 32 = 64° 

m(DBE) ve m(HBF) açıları eşittir.
180 + 64 = 244°
360 – 244 = 116°
İki açının toplamı → 116°
tek açı → 116 ÷ 2 = 58°dir.

a) Ölçüleri toplamı 90° olan komşu açı çiftlerini yazınız
Cevap:

m(FBH) ve m(CBF)
m(DBE) ve m(ABD)

b) Ölçüleri toplamı 180° olan komşu açı çiftlerini yazınız.
Cevap: m(ABH) ve m(CBH), m(ABE) ve m(CBE), m(ABH) ve m(ABE), m(HBC) ve m(CBE)

c) Komşu olmayıp ölçüleri toplamı 90° olan açı çiftlerini yazınız
Cevap: m(HBE) ve m(ABD), m(DBE) ve m(FBC)

ç) Komşu olmayıp ölçüleri toplamı 180° olan açı çiftlerini yazınız.
Cevap: m(CBE) ve m(ABH), m(HBC) ve m(ABE)

5. Sınıf Matematik Ders Kitabı Sayfa 53 Cevapları MEB Yayınları

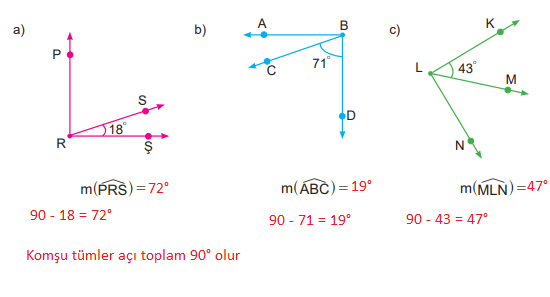
Örnek 5

Aşağıdaki açılar, komşu tümler açıdır. Verilenlerden yararlanarak istenen açının ölçüsünü bulunuz.
Cevap:

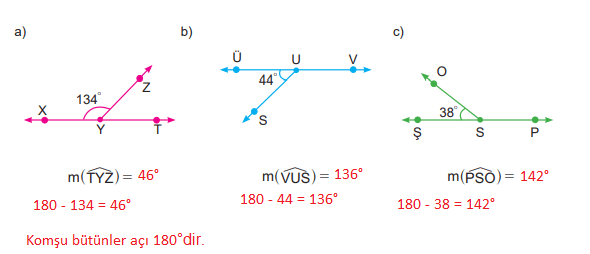
Örnek 6

Aşağıdaki açılar, komşu bütünler açıdır. Verilenlerden yararlanarak istenen açının ölçüsünü bulunuz.
Cevap:

Örnek 7

Aşağıdaki açıların tümler ve bütünler açı ölçülerini bulunuz.
Cevap: